امواج الیوت قسمت شانزدهم

امواج الیوت قسمت شانزدهم

 قانون تناوب

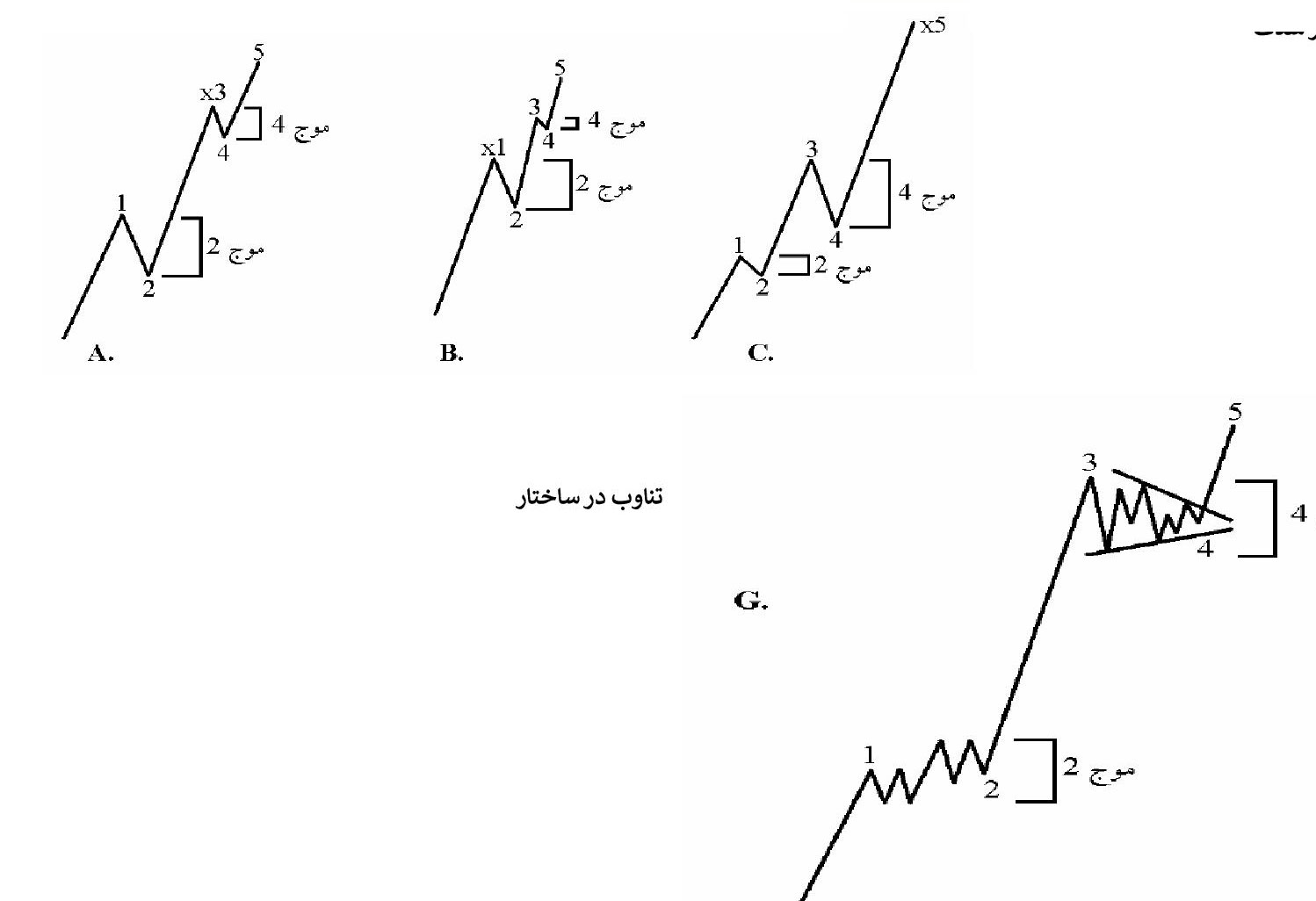
هنگام مقایسه موج های مجاور یا متعاقب از درجه یکسان بایستی به هر شکل ممکن متمایز و منحصر به فرد باشند. مهمترین عامل وجه تمایز زمان، قیمت، ساختار، شدت و پیچیدگی میباشد. بیشترین کاربرد قانون در رابطه با موج ۲ و ۴ میباشد.

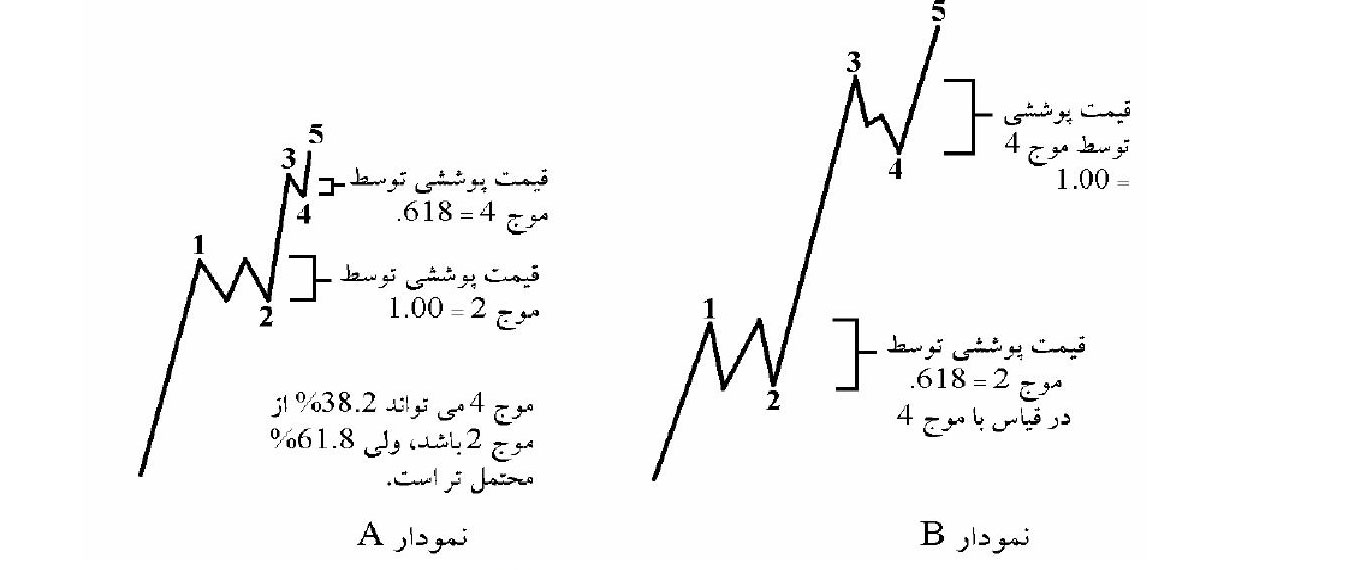
اگر موج ۲ بزرگترین موج اصلاحی در الگوی پیشرو باشد آنگاه موج ۴ به احتمال زیاد ۶۱/۸  و (یا ۳۸٫۲) درصد موج ۲ خواهد بود.

اگر موج ۴ بزرگترین موج اصلاحی در الگوی پیشرو باشد آنگاه موج ۲ به احتمال زیاد ۶۱٫۸ و یا( ۳۸/ ۲ )درصد موج ۲ خواهد بود.

تناوب در رشد

قانون تناوب درساختار موج A و B

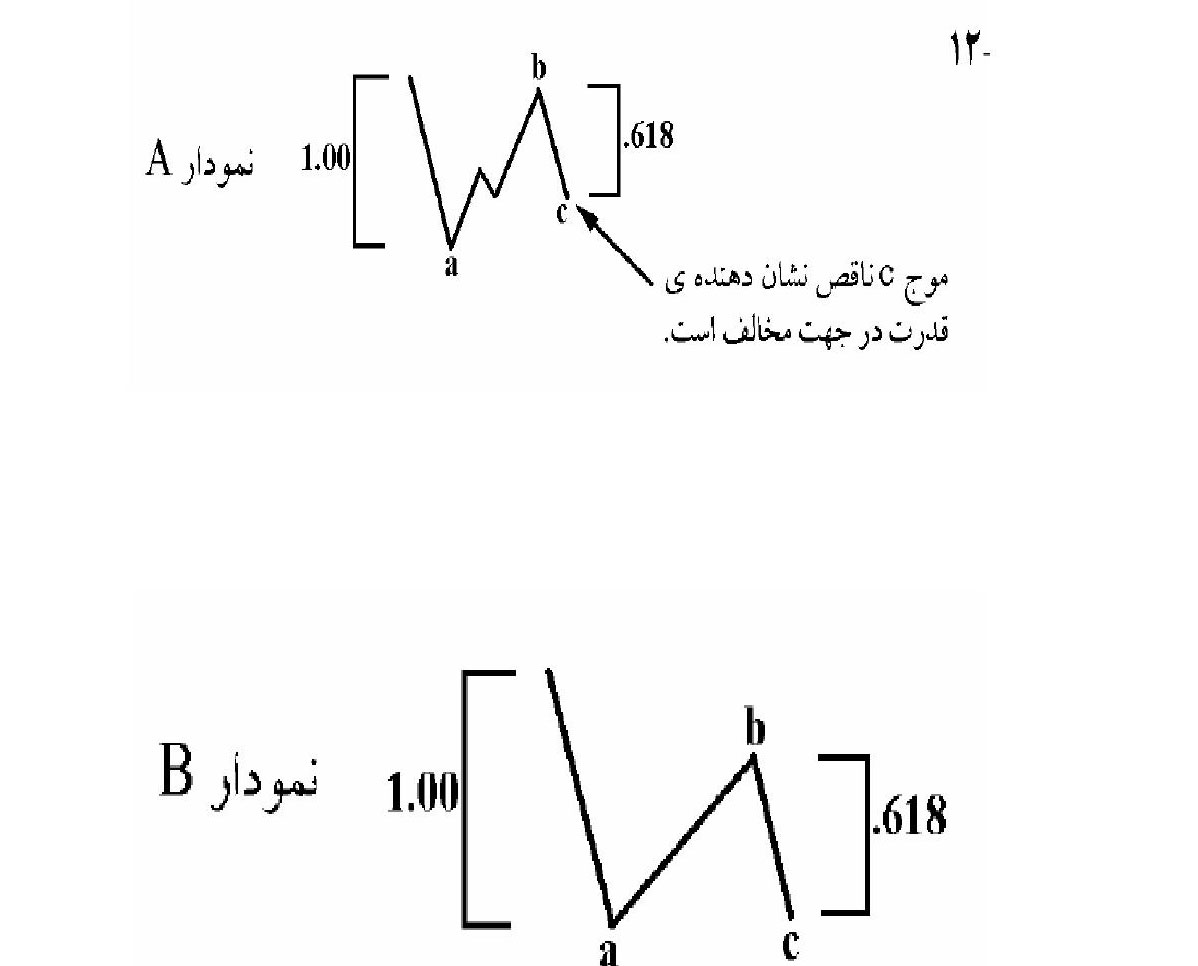
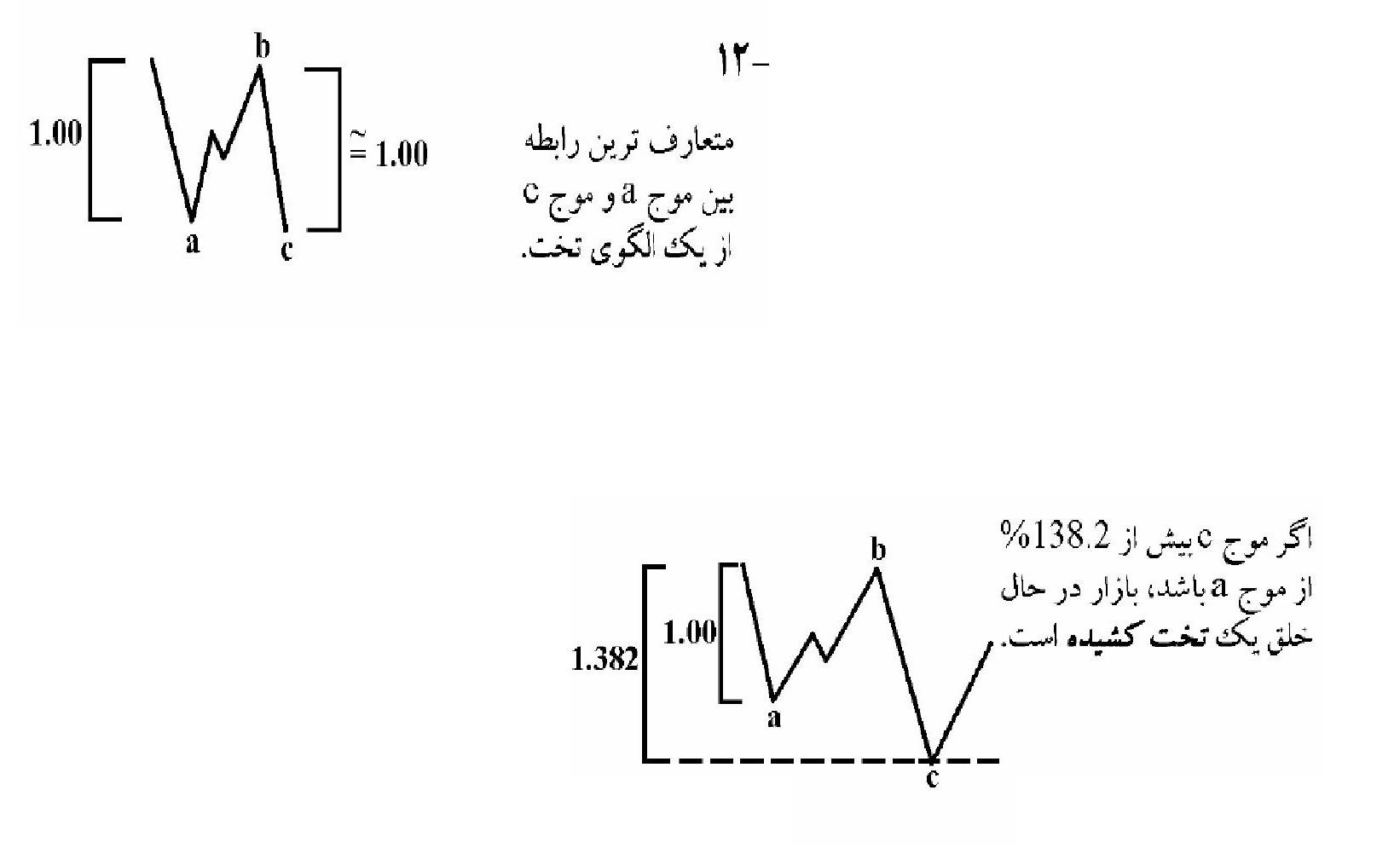
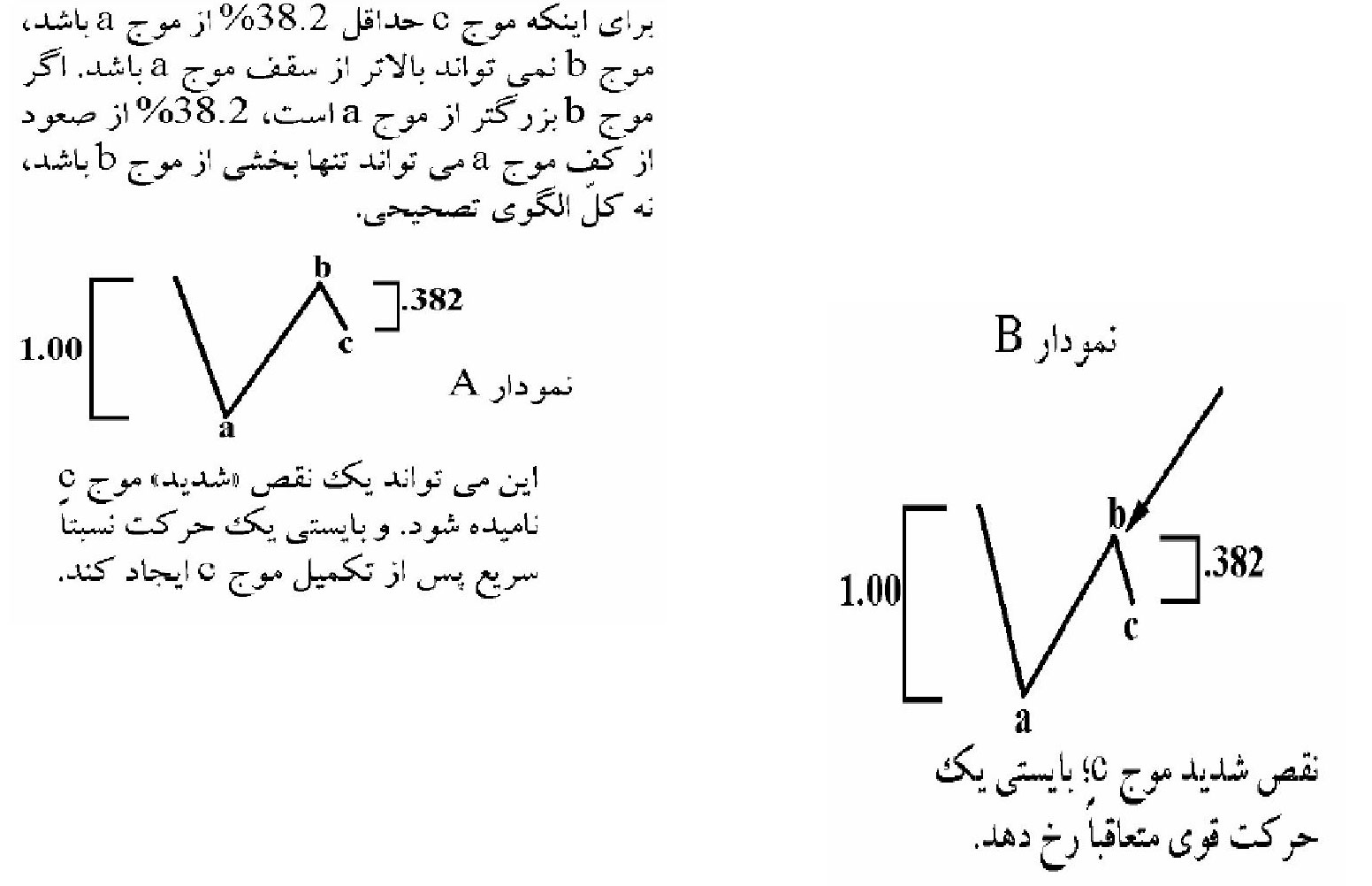
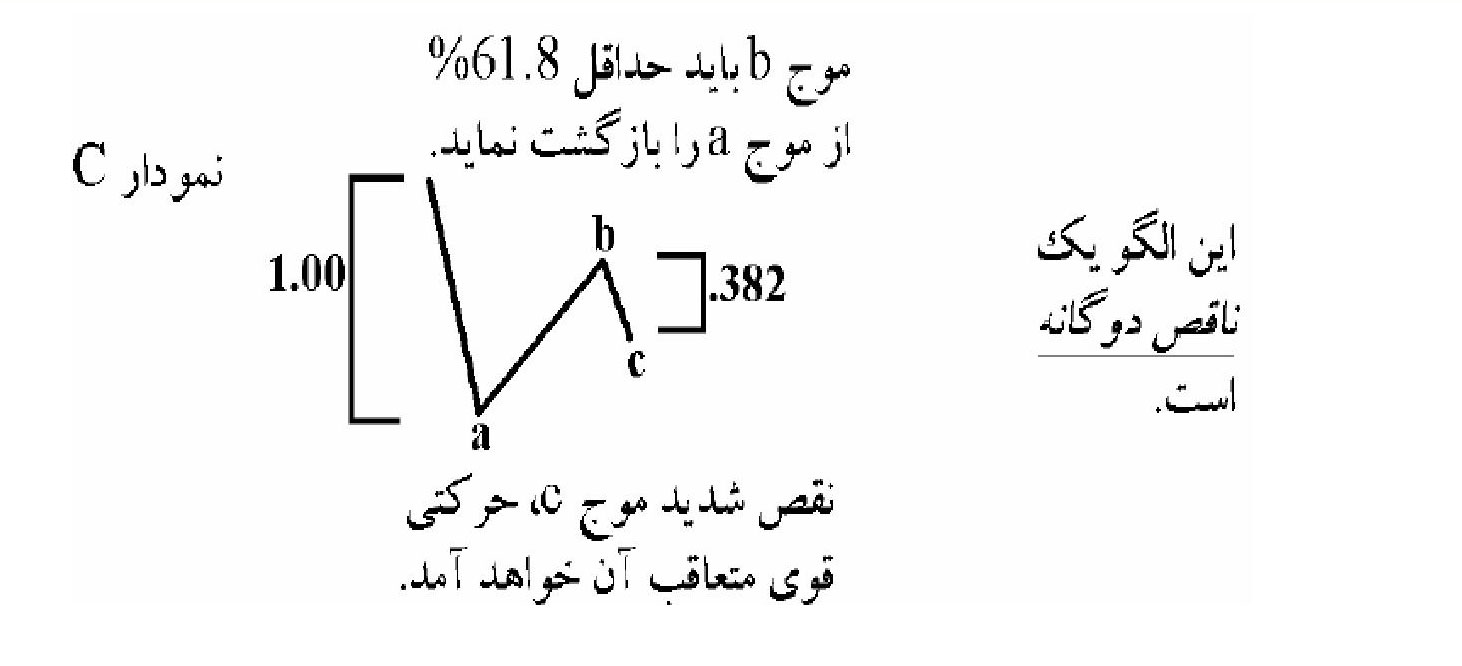
 قانون زمان

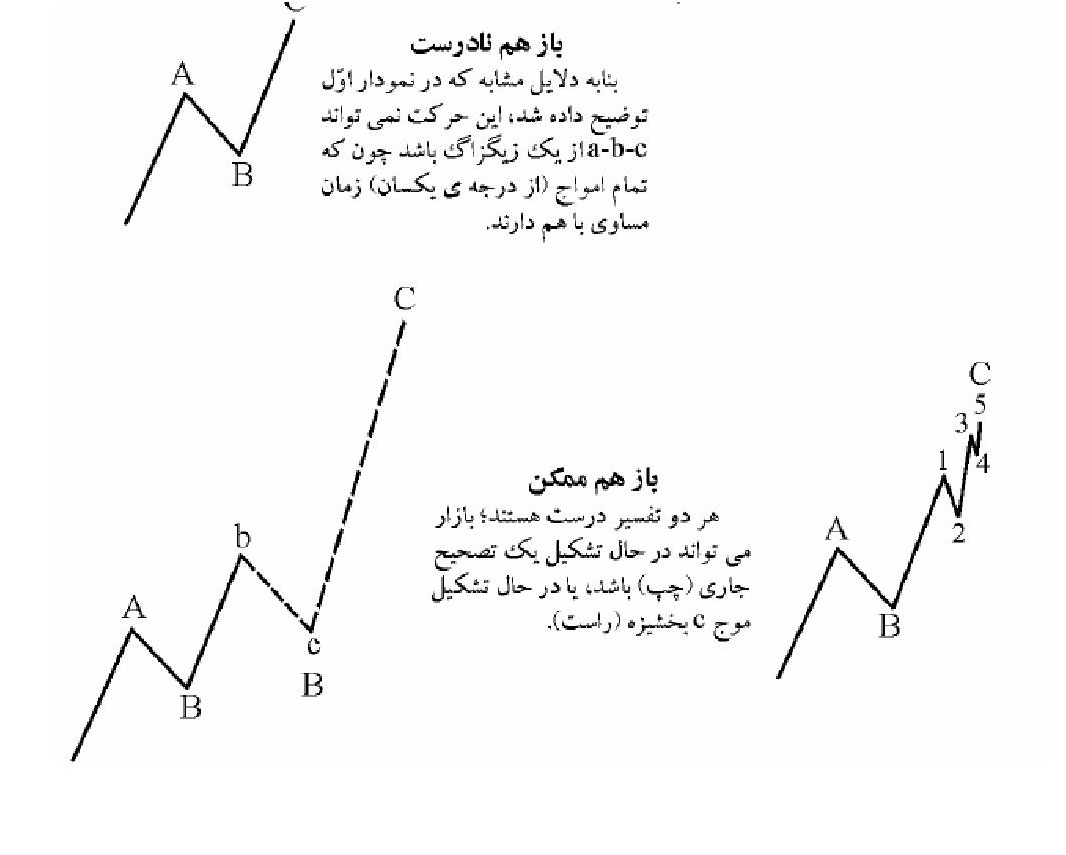
هیچ سه موج مجاور از درجه یکسانی، نمیتوانند تشابه زمانی داشته باشند. به بیان دیگر زمانی که سه موج مجاور دارای زمان مشابهی باشند در اینصورت موج سوم یا تکمیل نشده است یا سه موج مجاور از درجه یکسانی نمیباشند.

بر اساس قانون تشابه و تعادل، در یک تشابه زمانی بین دو موج مجاور، الگوی کوتاه مدت تر نمیبایستی کمتر از ۱/۳ ( از نظر زمانی با قیمتی) الگوی بلند مدت تر باشد.

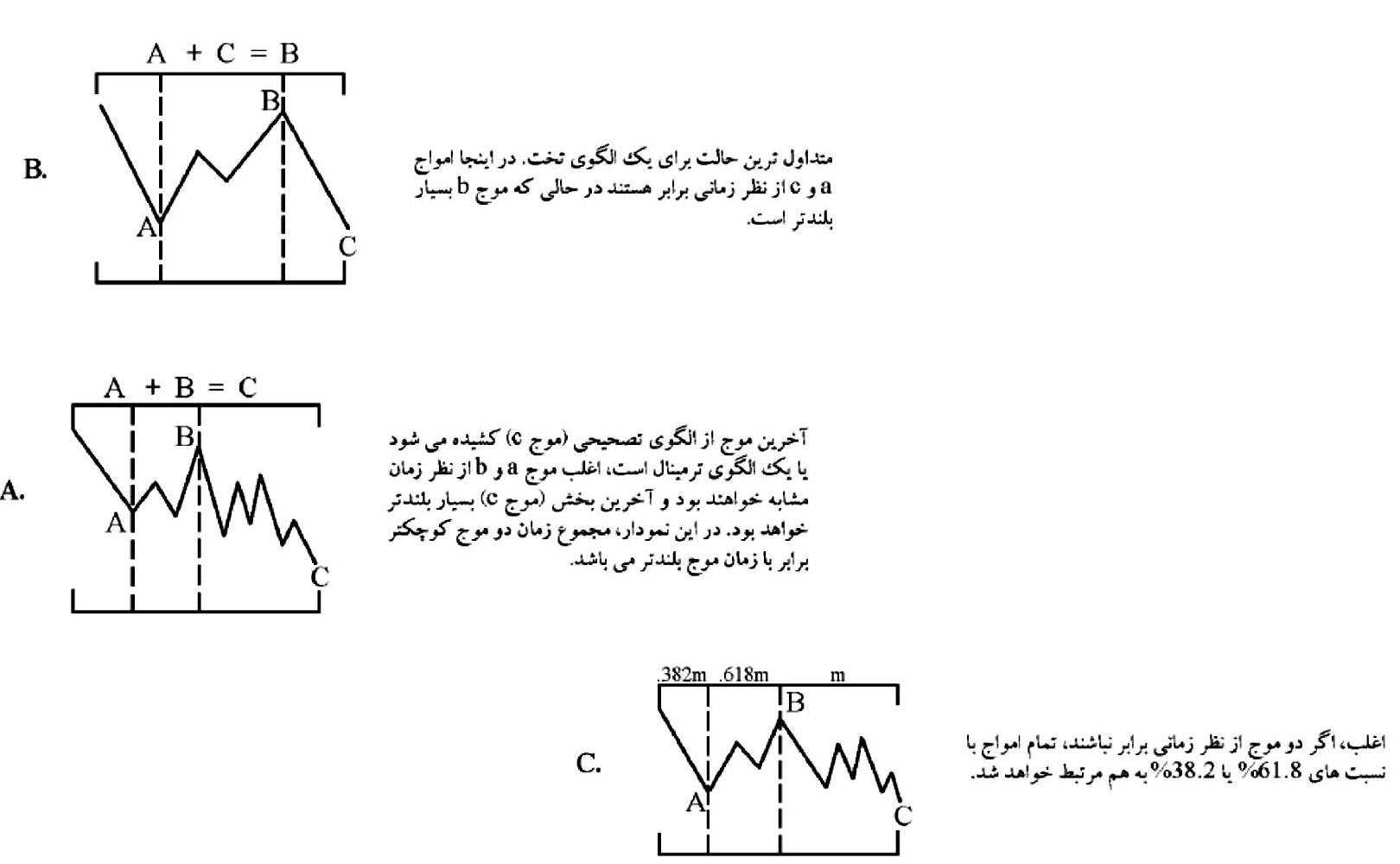
قانون برابری (Equality)

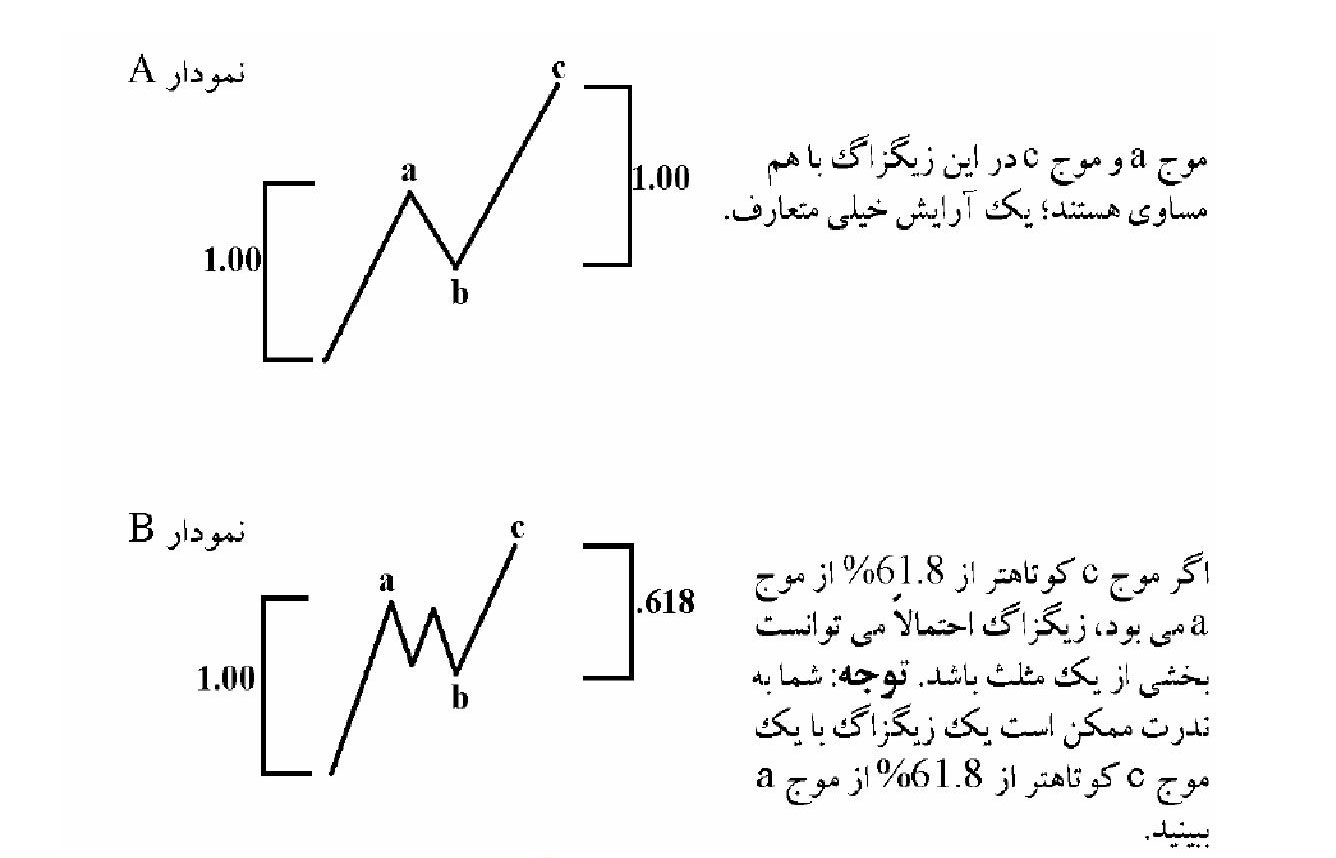
قانون برابری اظهار مینماید که دو موج غير ممتد بایستی از نظر زمانی و قیمتی گرایش به برابری داشته باشند و با یک نسبت فیبوناچی در بعد زمان یا قیمت باهم مرتبط باشند. این قانون بیشترین نمود را زمانی دارد که موج ۳ ممتد باشد و کمترین نمود را زمانی دارد که موج ۱ ممتد باشد.

•  اگر موج ۱ ممتد باشد قانون عطف به موجهای ۳ و ۵ میشود.
• اگر موج ۳ ممتد باشد قانون عطف به موجهای ۱ و۵ میشود.
• اگر موج ۵ ممتد باشد قانون عطف به موجهای ۳ و ۱ میشود.

درجه بندی پیچیدگی موجها .. انواع موج ها از نظر سطح پیچیدگی همانگونه که پیشتر اشاره شد موج های همسان میتوانند در درجه بندی امواج از یک درجه (و نه لزوما پیچیدگی یکسان) فرض شوند. ایده آل این است که موجهای از درجه یکسان هم از نظر زمانی هم از نظر قیمتی از قانون تشابه و تعادل پیروی کنند و لیکن زمانی که تشابه و تعادل قیمتی وجود نداشته باشد بازار تشابه و تعادل را از نظر زمانی ایجاد خواهد کرد و بالعکس. روش دیگر برای یافتن موج های از درجه یکسان استفاده از مبحث پیچیدگی میباشد. در این حالت موج های از درجه یکسان میبایستی از پیچیدگی یکسان یا مشابه برخوردار باشند. این روش در الگوهایی که از سطح پیچیدگی ۲ یا ۳ برخوردار میباشند مفید تر میباشد.

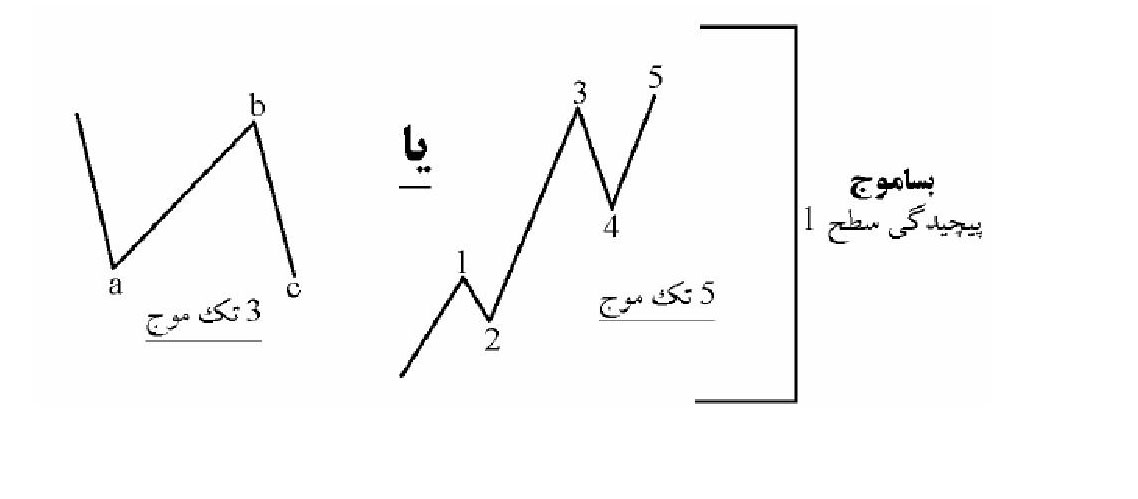
1.  تک موجها ( Mono -Waves ) : این موجها فاقد هرگونه ریزموجی میباشند و ازینرو درجه پیچیدگی این موجها صفر تعریف میشود.
2. بسا موجها ( Poly – Waves ): این موجها از ترکیب چند تک موج تشکیل میشوند. و از درجه پیچیدگی یک و یا بالاتر برخوردار میباشند. بر حسب درجه پیچیدگی عبارتند از:

• بسا موجهای ساده (Simple Poly – Waves ): تنها از سه تک موج (اصلاحی) یا پنج تک موج (پیشرو) تشکیل میشوند. درجه پیچیدگی آنها یک میباشد.
• بسا موجهای پیچیده (Complex Poly – Waves ): بخش اصلاحی در کل الگوی این نوع موجها دارای ریز موج میباشند ولیکن چون موجهای پیشرو در آنها همچنان فاقد ریزموج میباشند از درجه پیچیدگی یک برخوردار میباشند.

درجه بندی پیچیدگی موجها

انواع موج ها از نظر سطح پیچیدگی

همانگونه که پیشتر اشاره شد موج های همسان میتوانند در درجه بندی امواج از یک درجه (و نه لزوما پیچیدگی یکسان) فرض شوند. ایده آل این است که موجهای از درجه یکسان هم از نظر زمانی هم از نظر قیمتی از قانون تشابه و تعادل پیروی کنند و لیکن زمانی که تشابه و تعادل قیمتی وجود نداشته باشد بازار تشابه و تعادل را از نظر زمانی ایجاد خواهد کرد و بالعکس. روش دیگر برای یافتن موج های از درجه یکسان استفاده از مبحث پیچیدگی میباشد.

در این حالت موج های از درجه یکسان میبایستی از پیچیدگی یکسان یا مشابه برخوردار باشند. این روش در الگوهایی که از سطح پیچیدگی ۲ یا ۳ برخوردار میباشند مفید تر میباشد.

1.  تک موجها ( Mono -Waves ) : این موجها فاقد هرگونه ریزموجی میباشند و ازینرو درجه پیچیدگی این موجها صفر تعریف میشود.
2.  بسا موجها ( Poly – Waves ): این موجها از ترکیب چند تک موج تشکیل میشوند. و از درجه پیچیدگی یک و یا بالاتر برخوردار میباشند. بر حسب درجه پیچیدگی عبارتند از:

• بسا موجهای ساده (Simple Poly – Waves ): تنها از سه تک موج (اصلاحی) یا پنج تک موج (پیشرو) تشکیل میشوند. درجه پیچیدگی آنها یک میباشد.
• بسا موجهای پیچیده (Complex Poly – Waves ): بخش اصلاحی در کل الگوی این نوع موجها دارای ریز موج میباشند ولیکن چون موجهای پیشرو در آنها همچنان فاقد ریزموج میباشند از درجه پیچیدگی یک برخوردار میباشند.